Математические мозаики
Учимся делать мозаики
Геометрические преобразования и паркеты
Среди огромного разнообразия орнаментов выделяются "паркеты" (мозаики). Паркетом называют заполнение плоскости одинаковыми фигурами (элементами паркета), которые не перекрывают друг друга и не оставляют на плоскости пустого пространства (иногда паркетом называют заполнение плоскости несколькими фигурами, например, правильными многоугольниками). Тетрадный лист в клеточку представляет собой простейший паркет. Элементом паркета здесь является квадрат. Элементом паркета является также равносторонний треугольник, правильный шестиугольник, произвольный параллелограмм, даже произвольный четырехугольник. Можно придумать сотни, тысячи разных элементов паркетов. Некоторые из них изображены на рис. 1.
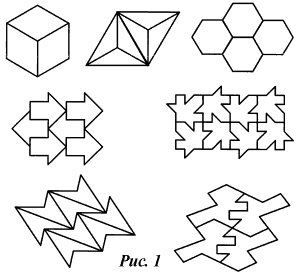
Придуманы паркеты, у которых несколько элементов образуют фигуру, подобную элементу паркета. Примеры таких паркетов приведены на рис. 2.
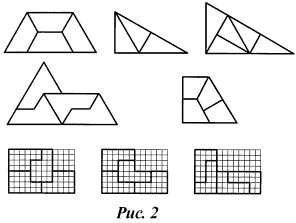
На рис. 3 приведен элемент простого паркета, который разбит на рисунке справа на четыре одинаковые фигурки - элементы нового паркета. А на рис. 4 показаны элементы нового паркета, также состоящие из четырех таких фигурок.
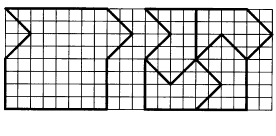
рис.3. |
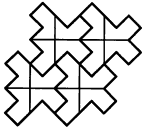
рис.4. |
На рис. 5 приведен паркет, элементами которого являются одинаковые пятиугольники с углами 90°, 120°, 60°, 240° и 30°, которые получились разбиением правильного шестиугольника. Из этих пятиугольников образованы фигуры. Для каждой из них проверьте, является ли она элементом паркета. Придумайте паркеты, элементы которых состоят из указанных пятиугольников.
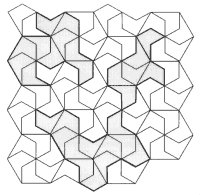
рис.5.
Всего существует 17 видов симметрии сетчатых орнаментов. Они схематично показаны на рис. 6 и 7. Первые семь из них (рис. 6, а-ж) допускают создание интересных паркетов без прямолинейных контуров.
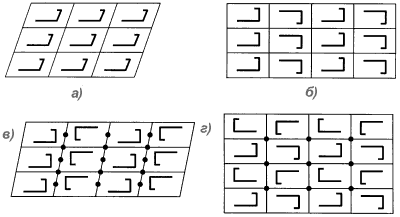
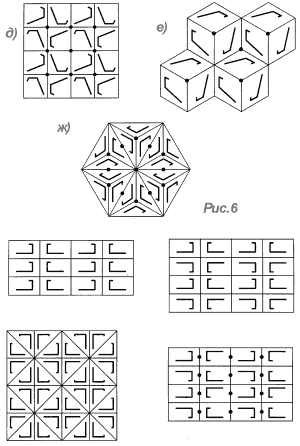
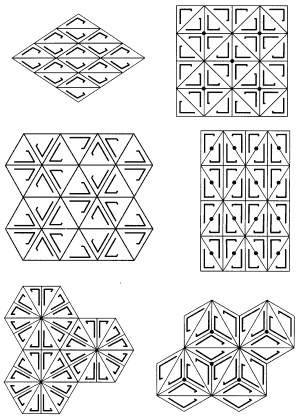
рис.7.
Паркеты являются прекрасным материалом для вовлечения учащихся в интересную, содержательную и поучительную деятельность при изучении некоторых тем школьного курса математики. В данном случае занимательность имеет не внешний, формальный характер, а побуждает учеников к выяснению сути изучаемого материала. Они с успехом могут быть использованы в 5-9-х классах на уроках и во внеурочное время. Замечательные паркеты придумывал знаменитый голландский художник Морис Эшер. Элементами паркета у него служили фигуры животных, птиц, рептилий.
Простейшим видом паркета является такой, в котором плоскость заполняется фигурами с помощью параллельного переноса.
Его общая схема приведена на рисунке 6,а. Такие паркеты полезно использовать при изучении параллельного переноса, привлекая и описание с помощью формул, т. е. алгебраический метод.
Задание 1.
На рис. 8 показан паркет, т. е. заполнение всей плоскости одинаковыми (равными) фигурами. Как видно из рисунка, этот паркет может быть совмещен сам с собой разными параллельными переносами, например, на три клетки вправо и на одну клетку вверх. Этот параллельный перенос задается парой чисел (3; 1). Данный паркет также совмещается сам с собой параллельным переносом, который характеризуется парой чисел (- 6; - 2), или парой (- 2; 3). Проверьте!
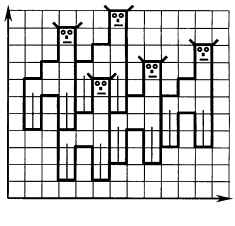
рис.8.
- Напишите еще 8-10 пар чисел, задающих параллельные переносы, совмещающие этот паркет с самим собой.
- Проделайте это для паркетов, которые можно получить параллельным переносом каждой из фигур, представленных на рис. 9.
- Проанализируйте для каждого паркета полученные пары чисел. Введите для них операции сложения, вычитания и умножения на целое число. Укажите две пары чисел такие, что остальные будут получаться из них с помощью введенных операций.
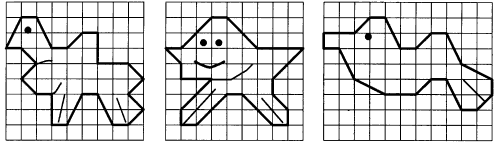
рис.9.
Задание 2.
Смещая параллельным переносом фигуру (рис. 10, а, б), заполните ею всю плоскость. Охарактеризуйте каждый паркет парами чисел - координатами векторов, которые задают параллельные переносы предложенной фигуры. Найдите сумму, разность двух любых полученных векторов или произведение этих векторов на целое число. Какой вектор получите в каждом случае? Будет ли параллельный перенос, задаваемый этим вектором, совмещать паркет с самим собой?
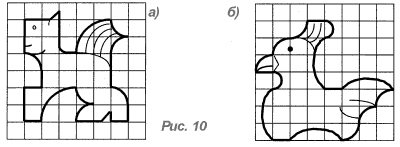
Приведенные два задания аналогичны между собой, хотя сформулированы на разных языках. Выполняя их, ученики обнаруживают тесную связь между параллельными переносами и векторами. В этих заданиях ясно прослеживается возможность разложения каждого вектора полученного векторного пространства по двум базисным векторам. Задания дают более осязаемые и легче понимаемые примеры операций векторов, вектора и числа.
Задание 3 (для шестиклассников).
Найдите координаты точек (x; y) - концов отрезков в контуре нарисованной фигуры (рис. 11). Затем найдите координаты (X; Y) новых точек по правилу: X = - x - 3, Y = y - 4. Соедините полученные точки в том же порядке.
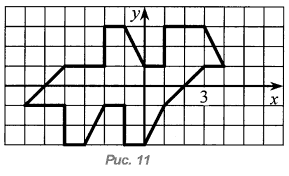
- Какая фигура получилась?
- Сместите данную и полученную фигуры на 7 единичных отрезков вправо или влево. Что у вас получилось?
- Заполните данной фигурой плоскость, получив паркет.
Задание 4.
Постройте фигуру, симметричную данной (рис. 12) относительно прямой a, а затем сместите полученную фигуру вниз на четыре клетки.
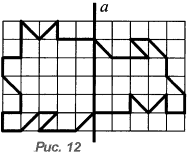
Заполните предложенной фигурой плоскость, получив паркет.
Фигуры на рис. 11 и 12 являются элементами паркета, общая схема которого показана на рис. 6 (б).
Задание 5.
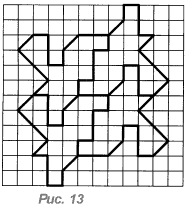
На рис. 13 показано заполнение плоскости фигурой, дающее паркет, общая схема которого показана на рис. 6,в. Определите центры симметрии этого паркета. Продолжите заполнение плоскости данной фигурой.
Задание 6.
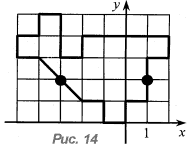
Постройте фигуру, симметричную данной относительно каждой из двух отмеченных точек (рис. 14). Заполните данной фигурой плоскость.
Задание 7.
Для каждой узловой точки фигуры, изображенной на рис. 14, найдите ее координаты (x; y) и постройте в той же системе точки с координатами (X; Y), найденными по формулам: X = - x - 6, Y = - y + 4. Соедините полученные точки в том же порядке. Что у вас получилось?
Задание 8.
- Укажите преобразования (одно или два), которые одну из фигур, представленных на рис. 15, переводят в другую.
- Введите систему координат и опишите в координатах одно из преобразований, совмещающее данный паркет с собой.
- Продолжите заполнение плоскости предложенной фигурой.
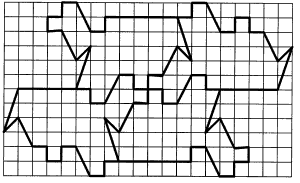
рис.15.
Задание 9.
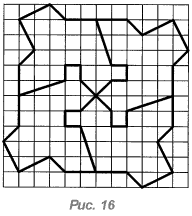
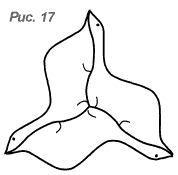
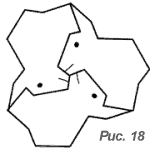
- На каждом из рис. 16-18 укажите центры поворотов, переводящих одну фигуру в другую.
- Заполните плоскость предложенными фигурами, получив паркеты видов E, F и G (рис. 6).
- Найдите центры симметрии полученных паркетов, если они есть.
Задание 10.
Каждой из фигурок на рис. 19 заполните плоскость, получив паркет. Для этого скопируйте фигурки на кальку.
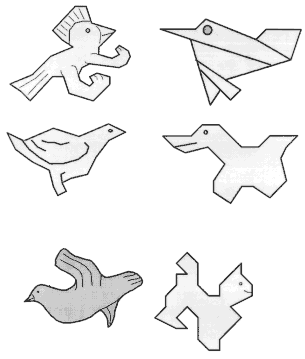
рис.19.
Задание 11.
Сравните фигурки на рис. 20. Скопируйте их на кальку и заполните плоскость, получив паркет.

рис.20.
Задание 12.
На рис. 21-36 представлены паркеты, придуманные автором (А. Цукарем, прим.). Изучите их строение и определите вид. Постройте многоугольник, равновеликий элементу паркета.
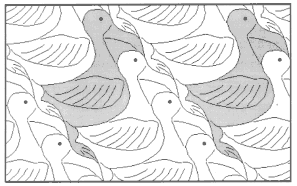
рис.21. |
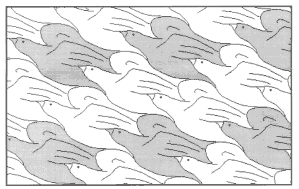
рис.22. |
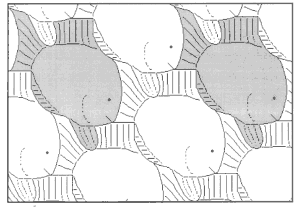
рис.23. |
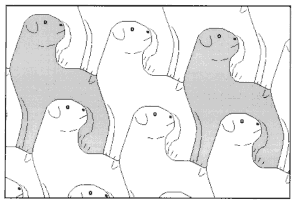
рис.24. |

рис.25. |
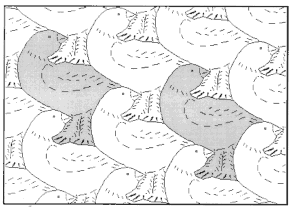
рис.26. |

рис.27. |
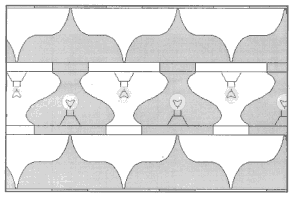
рис.28. |

рис.29. |
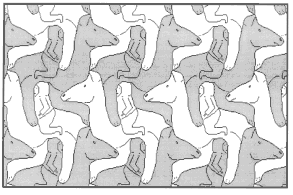
рис.30. |
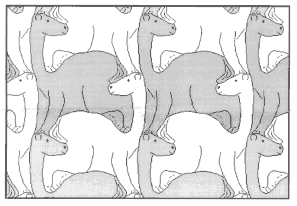
рис.31. |

рис.32. |
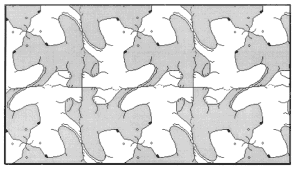
рис.33. |
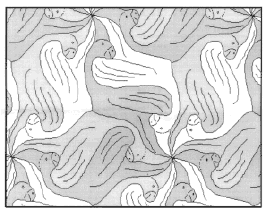
рис.34. |
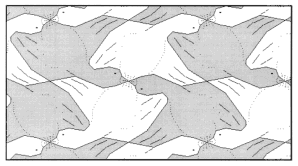
рис.35. |
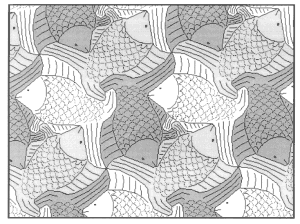
рис.36. |
Приведенные паркеты можно использовать разнообразно. В 5-6-х классах полезно предложить ученикам фигурку - элемент паркета, увеличенный и вырезанный из картона, с тем, чтобы они заполнили ею плоскость. Это способствует формированию у школьников геометрического видения.
При изучении координат и векторов используются задания, аналогичные приведенным выше. И, конечно, они естественно применимы при изучении геометрических преобразований.
Паркеты также можно использовать при изучении темы "Площади плоских фигур" для иллюстрации идеи, состоящей в том, что за единицу площади может быть выбрана произвольная (квадрируемая) фигура, например, элемент паркета, а также для нахождения многоугольника, указанного в задании 12.
Для паркета, изображенного на рис. 21, площадь фигурки (пеликана) равна площади параллелограмма с вершинами в точках, являющихся глазами четырех соседних птиц. Для остальных фигур такие многоугольники находятся без большого труда.
В заключение приведем паркет (рис. 37), в котором использованы три различные фигурки. Он получен из паркета, изображенного на рис. 33, заменой фигурок собачек новыми фигурками. Площади всех фигурок паркета равны.
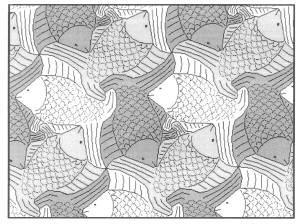
рис.37.
Автор: А. Цукарь, Новосибирск
