Масштабы вселенной
Продолжаем публикацию книги Р. Л. Грегори "Разумный глаз: Как мы узнаем то, что нам не дано в ощущениях".
Подобно тому как машины являются искусственным продолжением мышц человека, увеличивая их мощность и точность, измерительные приборы служат продолжением наших органов чувств. Приборы помогают человеку все дальше и глубже проникать во время и пространство и притом позволяют производить разные измерения в пределах системы шкал, построенных на основе общепринятых единиц измерения. Некоторые физические единицы мер возникли на основе величин, свойственных человеческому телу: фут приблизительно равен длине стопы взрослого человека, ярд близок к длине одного шага (Читатель без труда вспомнит русские аналогии: пядь, локоть, сажень и т.д. - Прим. перев)
Применять в качестве физических стандартов эталоны, которые "всегда под рукой", очень удобно, но, к сожалению, ни размеры частей тела разных людей, ни функции их органов чувств не могут быть достаточно одинаковыми. Такие эталоны годятся лишь для самых приблизительных оценок и, увы, совершенно не подходят ни для техники, ни для науки. В средние века был сделан следующий шаг к стандартизации мер длины: статистически определяли величину, равную 1 футу. Делалось это так. Измеряли длину стопы двенадцати мужчин, первыми покидавших церковь после воскресной утренней мессы; средняя величина (сумма длин всех двадцати четырех стоп, деленная на 24) принималась в качестве стандартной длины, равной 1 футу.
Познакомившись с некоторыми древними зданиями, мы можем утверждать, что еще за несколько тысячелетий до нашей эры с помощью простых инструментов проводились достаточно точные измерения; можно не сомневаться, что некоторые основные суждения, например об установке точных горизонтальных уровней, выносились не только на основе восприятия, но и путем рассуждений. Считается, что египтяне начинали строительство плоских горизонтальных фундаментов для больших зданий с того, что строили невысокую временную стенку и замкнутую ею площадь заполняли водой на высоту около десяти сантиметров: уровень воды служил указателем горизонтальности площадки. Человеческий разум приложил немало усилий, чтобы преодолеть физиологическую ограниченность человеческих органов чувств.
Ранние описания вселенной эгоцентричны; они основаны на сопоставлении ее параметров с физическими и функциональными возможностями человека. С появлением специальных измерительных приборов возникли другие меры; новые эталоны незаметно привели к тому, что центр вселенной уже не связывается в сознании людей с точкой, в которой находится наблюдатель. Стало известно, что во вселенной есть вещи, не только слишком малые или слишком далекие, чтобы их можно было отчетливо ощутить, но еще и скрытые от чувств, хотя и присутствующие в среде, непосредственно окружающей человека. Таков огромный диапазон электромагнитного спектра - от гамма-лучей до радиоволн; лишь одна его октава - видимый свет - доступна органам чувств, а через них и мозгу без всяких приборов.
Животному в окружающем его мире, обширном и большей частью враждебном, жизненно необходима способность к оценке размеров и расстояний; высокоразвитое зрение дает такую способность. В то же время сенсорные системы легко адаптируются - калибровка их часто нарушается. Несмотря на это, мы умеем определять "на глаз" соотношения размеров, а также интенсивность света; поэтому нам легко использовать и те физические стандарты измерений, где применяются инструменты вроде линеек, уровней, фотометров. Даже простые, но умело применяемые инструменты могут в тысячу раз улучшить точность перцептивных оценок, хотя природная чувствительность глаза и уха приближается к теоретическому пределу любого физически возможного детектора.
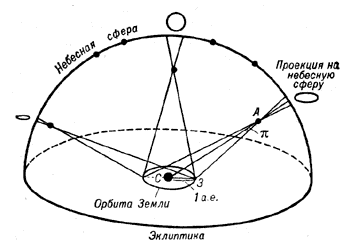
Определение расстояния до звезды А по ее видимому годичному перемещению на небесной сфере, вызванному движением Земли по орбите; π - параллакс звезды А, С - Солнце, З - Земля, расстояние междуними равно 1 а.е.
Когда сенсорная информация используется для руководства действием, задача состоит в том, чтобы контролировать с помощью этой информации движения в соответствии с положением и размерами окружающих предметов. Чтобы предсказание результатов действий и контроль эффективности этих действий были возможны, необходимо соразмерять разнородную сенсорную информацию в соответствии с воздействиями внешнего мира. Дело здесь обстоит точно так же, как в измерительной технике: шкалы инструментов не могут строиться произвольно, в конечном счете любая шкала должна быть основана на свойствах известных объектов. Некоторые измерения являются прямыми (например, измерение длины,` выполняемое с помощью линейки), другие - непрямыми (измерение температуры с помощью термометра).

Глаза сигнализируют о расстоянии до близких объектов способом, весьма похожим на тот, который применяют астрономы для измерения удаленности звезд.
Все единицы измерений основаны на выборе строго обусловленной процедуры, включающей правила изготовления точных линеек или, скажем, ламп со стандартной характеристикой излучения.
Рассматривая ход развития современных методов измерения, мы находим здесь глубокую аналогию с определенным периодом развития "непрямых органов чувств" - зрения и слуха, возникших уже после появления "прямых органов чувств" - осязания и вкуса, непосредственно контролирующих жизненно важные отношения с окружающим миром. Видеть - значит интерпретировать каждый полученный паттерн в соответствии с предполагаемым устройством мира реальных объектов; та же задача ставится перед всеми непрямыми способами научных измерений. В обоих случаях выдвигаются и затем проверяются альтернативные гипотезы - чтобы отклонить все, кроме одной. В обоих случаях отдельные измерения должны быть связаны с единой шкалой измерений, выведенной либо из результатов применения прямых методов измерений, либо из допущений, основанных на гипотезе о природе измеряемых объектов.
Разовьем дальше тезис о логическом сходстве зрения с непрямыми методами измерения в физике. И здесь и там необходимы допущения. И здесь и там велика зависимость от прямых измерений. И здесь и там необходимы константы - эталоны для построения шкал, выведенные на основе анализа прошлых успехов и неудач измерения реального мира. Возьмем какой-нибудь пример научного измерения и детально разберем его. Посмотрим, например, как измеряются звездные расстояния.
Для измерений звездных расстояний астрономы применяют оба метода измерения - прямой и непрямой. Но применимость прямого измерения ограничена немногими ближайшими к нам звездами. В отношении более далеких звезд необходимо делать некоторые допущения, причем всегда приходится считаться с тем, что эти допущения могут оказаться ошибочными. ,-
Метод прямого измерения расстояний до звезд эквивалентен стереоскопическому зрению. Это геометрический способ, его результаты, как и результаты стереоскопического восприятия, в основном однозначны; тем не менее это довольно тонкий способ, и даже незначительные погрешности приборов могут сильно сказаться на результатах. Метод состоит в измерении кажущегося смещения ближних звезд относительно дальних при смене точки наблюдения (тригонометрический параллакс). При стереоскопическом зрении различие точек наблюдения задано постоянным расстоянием (базисом) между глазами - оно равно приблизительно 60 миллиметрам. Но для астрономов даже поперечник Земли - недостаточный базис при измерении звездных расстояний. Замеры они проводят не одновременно, а с интервалом в шесть месяцев; в качестве базиса используется поперечник земной орбиты (около 300 миллионов километров). Этим способом было впервые измерено расстояние до звезды; немек кий астроном Бессель в 1838 году измерил удаленность звезды 61 Лебедя2^. Его результат составил 0,35" (в угловых секундах). Уточненный позднее результат равен 0,30". Такой параллакс соответствует расстоянию около десяти световых лет. Наибольший известный параллакс - меньше 1"; такой параллакс, к примеру, может быть получен, если наблюдать предмет 25 миллиметров в поперечнике с расстояния около пяти километров. Прямой метод измерения параллакса позволяет измерять расстояния в пределах около 300 световых лет (хотя Туманность Анд >меды, до которой около двух миллионов световых лет, можно увидеть и невооруженным глазом).
Измерение расстояний в световых годах связано с измерением параллакса лишь косвенно. Правда, есть и такая единица, которая связана с параллаксом непосредственно, - "парсек" Один парсек - это расстояние, соответствующее годичному пар. шаксу I"3`; оно равно произведению радиуса земной орбиты на число 206 265; радиус земной орбиты (среднее расстояние до Солнца, равное 150 миллионам километров) является астрономической единицей расстояния.
Сам термин "парсек" произведен от слов "параллакс, равный одной секунде"; итак, 1 парсек равен 206 265 астрономическим единицам, или 3,258 светового года. До ближайшей к нам звезды 1,31 парсека, или 4,2 светового года.
Для сравнения укажем, что стереоскопическое зрение действует на расстояниях до нескольких сотен метров. Столь малый радиус действия объясняется двумя причинами: первая состоит в том, что разрешающая способность глаза примерно в сто раз ниже, чем соответствующая характеристика для телескопа; вторая (и более важная) - расстояние между глазами (базис стереозре-ния) - является ничтожной величиной по сравнению с диаметром орбиты Земли.
Наибольшие звездные расстояния, при которых еще возможны определения тригонометрических параллаксов, близки к 100 парсекам. При еще больших удаленностях применяется способ, известный под названием "определение средних параллаксов"; в его основе лежит тот (эмпирически установленный) факт, что Солнце (и Земля вместе с ним) перемещается в пространстве относительно большого числа звезд по направлению к Веге в созвездии Лиры. Перемещение Солнца порождает у наблюдателя ощущение смещения близких к нам звезд; их кажущееся движение характеризуется некоторой кажущейся скоростью, а величина последней зависит от расстояния каждой звезды. Это точная аналогия кажущегося движения ландшафта, наблюдаемого из окна идущего поезда: ближняя зона местности "движется" быстрее, чем отдаленная. Поскольку наблюдение перспективного смещения звезд производится в течение ряда лет (к нашим дням период накопления точных фотографий звездного неба насчитывает почти сто лет), появляется возможность оценки звездных расстояний, намного превышающих те, что доступны прямым тригонометрическим методам, использующим в качестве базиса диаметр земной орбиты. Для этого совершенно необходимо, однако, отличать изменение положения звезд, возникающее вследствие движения Солнца (и Земли вместе с ним) по направлению к Веге, от относительного "собственного движения" отдельных звезд. Движение Солнца сквозь пространство выводится статистически из результатов наблюдений кажущегося движения очень большого числа звезд; остаточное систематическое движение приписывается подлинному движению Солнца. Вывести величины, характеризующие движение солнечной системы среди звезд, - дело сложное; оно требует большого числа наблюдений и большой вычислительной работы. Между тем совершенно таким же делом занят мозг человека, движущегося сквозь многолюдную площадь, или управляющего автомобилем в густом потоке движения, или ведущего самолет в строю других самолетов. Пределы способности мозга к обработке величин и направлений скоростей, заданных меняющейся перспективой множества объектов, движущихся относительно некоторой поверхности, неизвестны. Исследовать это было бы чрезвычайно интересно.
Расстояния до далеких звезд приходится измерять непрямыми способами, при которых применять геометрию уже нельзя. Все эти способы основаны на некоторых допущениях, не поддающихся прямой проверке.

В этом звездном скоплении видны объекты весьма разной яркости. В среднем чем дальше звезда, тем меньше ее блеск, но некоторые тусклые звезды на самом деле находятся близко, только их собственная светимость мала. Они кажутся далекими, но в действительности это не так
Ясно, что если бы собственная светимость всех звезд была одинакова, то относительные расстояния до звезд можно было бы узнать довольно легко, исходя из универсального закона, связывающего блеск звезды с расстоянием до нее (видимый блеск обратно пропорционален квадрату расстояния). Но светимость звезд (их "абсолютная звездная величина") очень сильно варьирует, и поэтому видимый блеск звезды может служить лишь очень приблизительной оценкой ее удаленности. Все же звезды поддаются классификации: исходя из спектров звезд (и еще некоторых величин), их можно разбить на группы с известной светимостью. Тогда становится возможной и оценка расстояний по видимому блеску - при условии, что применяются верно выбранные константы для построения шкал оценки светимости звезды и учитываются все факторы, обусловливающие потерю света на пути от звезды к наблюдателю. Свет может ослабеть, проходя сквозь облака межзвездного газа, и это надо обязательно учитывать, чтобы не возникло ошибки в оценке расстояния, основанной на видимом блеске звезды. Неверно выбранная константа шкалы приведет к ошибке - и она будет похожа на те ошибки в оценке расстояний, которые совершаются зрением в тумане или в дыму.
Итак, необходимо сделать некоторые обоснованные допущения о самом объекте, о помехах на пути от объекта к наблюдателю и, наконец, о свойствах и калибровке самих измерительных приборов, прежде чем применять непрямые методы измерения, не опасаясь, что при этом возникнет систематическая ошибка. Ошибки такого рода, по-видимому, эквивалентны ошибкам перцептивного шкалирования, вследствие которых возникают иллюзии искажения.
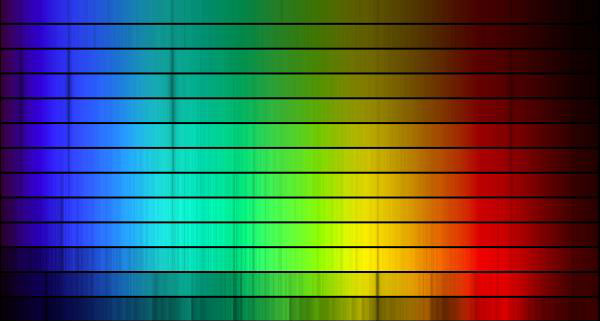
Астрономы разделяют звезды на различные спектральные классы. Спектральная классификация, разработка которой началась в XIX веке, первоначально была основана на интенсивности линий поглощения водорода. Классы, которые наилучшим образом описывают температуру звезд, используются и в настоящее время. Типичные спектры для семи основных спектральных классов - OBAFGKM - показаны на картинке: вверху - спектр звезды класса "O", а далее для каждого класса приводится по два спектра, причем для каждого последующего спектра температура звезды ниже. Для запоминания этой последовательности букв принято использовать мнемоническую фразу "Oh Be A Fine Girl/Guy Kiss Me (О, будь хорошей девочкой/хорошим парнем и поцелуй меня)". (В русском языке наиболее известна фраза "Один Бритый Англичанин Финики Жевал Как Морковь). При проведении конкурса среди учащихся было предложено несколько других, более или менее политически корректных фраз, например "Oven Baked Apples From Grandpa`s/Grandma`s Kitchen. Mmmm (Запеченные в печи яблоки из дедушкиной/бабушкиной кухни. Мммм.)" Наше Солнце имеет спектральный класс "G".
Объекты, еще не классифицированные и потому не имеющие надежных оценочных констант, причиняют крупные неприятности астрономам. Так, например, в отношении недавно открытых звездных объектов - квазаров - не известно, являются ли они необычайно мощными источниками излучения, лежащими на огромных расстояниях от нас, или светимость их средняя, а значит, и расстояния - обычного порядка. В данном случае трудность возникла потому, что в спектрах квазаров зарегистрировано красное смещение, которое обыкновенно указывает на очень большую скорость удаления (смещение возникает в результате эффекта Доплера, наличие которого само по себе свидетельствует о большой удаленности объекта). Красное смещение, наблюдаемое у квазаров, может объясняться либо огромной их удаленностью, либо другими причинами. До сих пор не решено, как следует выбирать константы шкалирования для измерения квазаров; поэтому нет согласия и в вопросе о том, являются квазары очень яркими и очень далекими объектами или средними по интенсивности излучения и соответственно менее удаленными; в последнем случае должна существовать особая причина, ответственная за неподчи нение квазаров тем общим допущениям, которые оказываются справедливыми при измерении расстояний до других звездных объектов.
Быть может, читателю покажется, что мы совершаем слишком смелый прыжок, заявляя, что положение вещей с квазарами в астрономии логически подобно той особой проблеме, которую ставят перед глазом картины, воспринимаемые зрением. Но в картинах действительно есть весьма сходные сомнительные моменты шкалирования. Ретинальное изображение картины содержит перспективу, но заданную не геометрическим сокращением размеров и формы предметов с увеличением расстояния (поскольку картина плоская); налицо как раз такая ситуация, при которой должны возникнуть большие ошибки в физических измерениях, поскольку допущения, обычно вполне надежные, здесь не годятся. Нормальные условия неизбежно нарушают точность непрямых измерений; с этой точки зрения картины могут оказаться совсем никудышными объектами, поскольку в некоторых случаях (вспомните Пильтдаунский череп. Автор имеет в виду историю знаменитого антропологического подлога. В 1909 году некий Чарлз Даусон "открыл" фрагмент "древнего человеческого черепа" (близ Пильтдауна, в графстве Сассекс); в том же месте были найдены затем еще несколько фрагментов, в том числе сенсационный зуб. Лишь спустя 45 лет (!) было доказано, что все признаки "древности" черепа - дело рук нашего современника. Подробности читатель может найти в книге: Эйдельман Н. Ищу предка. М.: Молодая гвардия, 1970. - Прим. перев.) неверные указания могут быть даны намеренно, чтобы обмануть глаз. Картины подают на вход зрительной системы до такой степени искусственную информацию, что приходится удивляться вовсе не тому, что картины иногда оказываются неоднозначными, неопределенными, парадоксальными или искаженными, а, напротив, тому, что мы вообще что-либо разбираем в них.
Астрономические объекты - это тоже особые объекты зрительного восприятия; в их отношении мы не можем воспользоваться надежным перцептивным шкалированием, константы которого выводятся из прямых измерений.

Свет отдаленных звезд проходит сквозь огромные газоыме облака в созвездии Ориона. Это может привести к ошибке при оценке звездных расстояний на основе измерения светимости звезд, если не будет внесена поправка, основанная на сведениях о поглощении света
Как мы измеряем Луну и звезды?
Вопрос о восприятии Луны интересен, потому что до недавнего времени человек не приближался к ней никогда. Размер ретинального изображения Луны довольно велик (0,5 градуса, а это примерно четверть диаметра центральной - "фовеальной" - области сетчатки). Даже невооруженный глаз различает на поверхности Луны некоторые детали, к тому же в отличие от Солнца Луна имеет приятную для прямого наблюдения яркость. Тот факт, что мы не можем просто так прогуляться к Луне и потрогать ее руками, делает Луну прямо-таки небесным даром исследователю восприятия, а наблюдения космонавтов лишь помогают в этом деле.

На фотографии изображен второй человек, ступивший на поверхность Луны, - Эдвин Алдрин по прозвищу "непоседа". Космический корабль "Аполлон-11" доставил людей на Луну. Нейл Армстронг и Эдвин Алдрин ходили по поверхности Луны, в то время как Михаель Коллинс летал над ними в командном модуле. Эта первая команда водрузила на поверхности Луны табличку с надписью: "В этом месте в июле 1969 года от рождества Христа человек с планеты Земля впервые ступил на Луну. Мы выступаем за мир во всем Мире". С помощью космических кораблей "Аполлон" стали возможным полеты и высадка астронавтов на Луну , а также их безопасное возвращение на Землю.
Разумное представление о расстоянии до Луны и о ее размерах существует по крайней мере последние 2 000 лет, со времен Гиппарха. Всем образованным людям известно, что расстояние от Луны до Земли - около 400 000 километров, что диаметр Луны равен примерно 3 500 километрам и что форма ее близка к шару. Но воспринимается Луна совсем иначе, и даже самое точное знание не помогает воспринять Луну в ее подлинном виде. Она кажется диском (примерно 30 сантиметров в поперечнике) и удалена "на глаз" всего километра на полтора или около того. Похоже, что все люди приблизительно одинаково воспринимают размеры и удаленность Луны, то есть все мы зрительно оцениваем Луну примерно с одной и той же ошибкой. Самая массовая и самая огромная иллюзия в истории человека!
Фактически мы ошибаемся в оценке размеров и удаленности Луны в миллион раз! Удивительна, однако, не только эта гигантская иллюзия; странно, что наше зрение вообще содержит оценку размера и удаленности Луны. Ведь зрение по самому своему существу является источником непрямого сигнала о размере и расстоянии; логически необходимо исходить из того, что калибровка ретинальных изображений осуществляется на основе прямых измерений - прикосновений к объекту, числа шагов или времени движения до объекта (при этом регистрируются изменения размеров изображения на сетчатке по мере сближения с объектом), но калибровка такого рода невозможна по отношению к объекту "Луна". Тот факт, что мы все же воспринимаем Луну как объект, имеющий вполне определенные размеры и находящийся на определенном расстоянии, означает, по-видимому, что перцептивная гипотеза приписывает Луне признаки, основываясь на аналогиях с земными, знакомыми объектами. Вероятно, воспринимаемые размеры и расстояние заданы в случае Луны неким усреднением этих признаков, взятых по всем объектам, которые дают столь же небольшое ретинальное изображение. Во всяком случае, сам факт наличия перцептивно определенного размера и расстояния показывает, что перцептивная система при отсутствии ясной информации принимает искусственную оценку, отказываясь от альтернативы - оставить объект вообще вне шкалы оценок.
Хорошо известно, что Луна обычно кажется сильно увеличенной, когда она низко над горизонтом. По-видимому, перспектива и другие признаки расстояния, связанные с видимой поверхностью Земли, влияют на оценку размера Луны, смещая "нуль шкалы размеров".

На фотографии изображена полная Луна, восходящая над греческим мысом Сауньон . На переднем плане стоит храм Посейдона , который был построен 24 столетия назад для моряков, плывущих по Эгейскому морю.
Возможно, есть нечто удивительное в том, что четкое-знание подлинных физических параметров Луны не влияет на величину ее видимых параметров. Ведь восприятие - это своего рода процесс решения проблем; очевидно, в данном процессе логическое знание мало влияет на выбор решения.
Тот факт, что Луна кажется больше, когда стоит низко над горизонтом, заинтересовал еще Птолемея. Он предположил, что низкая Луна воспринимается дальше линии горизонта, а высокая - ближе, отсюда разница в видимых размерах. Фактически Птолемей предложил объяснение в духе закона Эммерта). Закон Эммерта, установленный способом наблюдения, гласит: "При неизменной величине ретинального изображения воспринимаемый размер предмета прямо Пропорционален воспринимаемому расстоянию до предмета". - Прим. перев. Но это неверно; обсуждаемый случай не согласуется с законом Эммерта: на самом деле Луна, расположенная над горизонтом, кажется одновременно и больше и ближе. Мы могли бы сказать, что причину тут следует искать в рамках процесса первичного шкалирования величин в зрительной системе; увеличение видимого размера без увеличения видимой удаленности похоже на то, что происходит при иллюзиях искажения. Нам следует ожидать именно кажущегося уменьшения удаленности Луны, когда ее видимый размер возрастает, аналогично тому, как воспринимается в темноте любой светящийся объект.
Греки считали, что звезды - это светящиеся точки, вкрапленные в поверхность вогнутой сферы, центром которой является Земля. Мы все еще видим вселенную именно так, хотя и знаем, что она совсем другая. Мы видим Солнце, движущееся поперек неба, хотя знаем, что причина этого кажущегося движения Солнца - собственное вращение Земли.
Находясь в движении, мы замечаем, что Луна и звезды "сопровождают" нас в пути. Разумом мы понимаем, что они неподвижны, но так далеки, что параллактическое смещение их не может быть нами замечено. Земные же предметы остаются на вид неподвижными (параллакс их смещения слишком мал) только в тех случаях, когда предметы перемещаются вместе с нами; потому и небеса зрительно "сопровождают" нас в пути. Быть может, меня не сочтут слишком большим фантазером, если я допущу, что именно видимое активное участие небес в перемещениях человека привело его к вере в то, что звезды не холодные созерцатели земной суеты, а заинтересованные наблюдатели всех ее индивидуальных судеб.
Далее в выпусках:
- Неоднозначные, парадоксальные и неопределенные фигуры
- Фигуры, содержащие искажения формы
- Рисование на плоскости
- Рисование в трехмерном пространстве
- Картины, символы, мысль и язык
- Зримая суть вещей
При поддержке yugzone.ru
